The following statements are equivalent: b is divisible by a. Let a and b be two integers such that a 0. Show that if \(a\mid b\) and \(b\mid a\) then \(a=\pm b\). In this section, we shall study the concept of divisibility.Show that if \(ac\mid bc\), then \(a\mid b\).Show that the square of any integer is of the form \(3m\) or \(3m+1\) but not of the form \(3m+2\).
Show that the square of every odd integer is of the form \(8m+1\). It arose in Latin America in the 1960s, became influential in academic circles and at regional organizations, spread rapidly to. Show that if \(m\) is an integer then \(3\) divides \(m^3-m\). Dependency theory is a school of thought in contemporary social science which seeks to contribute to an understanding of underdevelopment, an analysis of its causes, and to a lesser extent, paths toward overcoming it. Show that the product of two even integers is even, the product of two odd integers is odd and the product of an even integer and an odd integer is even. Prove that the sum of two even integers is even, the sum of two odd integers is even and the sum of an even integer and an odd integer is odd. Show that if \(a\) and \(b\) are positive integers and \(a\mid b\), then \(a\leq b\). Show that if \(a,b,c\) and \(d\) are integers with \(a\) and \(c\) nonzero, such that \(a\mid b\) and \(c\mid d\), then \(ac\mid bd\). Use the division algorithm to find the quotient and the remainder when -100 is divided by 13. Use the division algorithm to find the quotient and the remainder when 76 is divided by 13. If a and b are integers with a 0, we say that a divides b if there exists an. Show that \(5\mid 25, 19\mid38\) and \(2\mid 98\). The issue of divisibility is addressed in the following definition. Now if \(r\geq b\) then (since \(b>0\)) \ This leads to a contradiction since \(r\) is assumed to be the least positive integer of the form \(r=a-bq\). By the well ordering principle, \(A\) has a least element \(r=a-bq\) for some \(q\). Keep doing this until you can no longer divide.\( \newcommand\) is such that \(|b|0\), then there exist unique integers \(q\) and \(r\) such that \(a=bq+r\) where \(0\leq r0\). When 3 does not work anymore, divide by 4. When 2 does not work anymore, divide by 3. Their greatest common divisor is again the largest integer dividing all of the integers in the set. (If 2 does not work, start with 3 instead, and so forth) Keep dividing by 2 until 2 does not work anymore. GCF(30,50) Technique: Start by dividing each number by 2. The factors for 12 are 1, 2, 3, 4, 6, and 12 The common factor is 1 The largest number both factors have in common is 1, so GCF(7,12) = 1 Method #2: My teacher's method: find gcf of 16 and 24 There is another example on the right to ensure that you understood this technique. Find GCF(7,12) The factors for 7 are 1 and 7. The largest factor for both numbers have in common is 8, so GCF(16,24) = 8. Find the intersection of the two sets or simply the common factors. The factors for 16 are 1, 2, 4, 8, and 16. Method #1: Set intersection method: First, list the factors of each number as a set. For instance, find GCF of 16 and 24 written as GCF(16,24). Here, we will concern ourselves with just 2 The GCF of two numbers is the largest factor of the two numbers. Whenever you are talking about greatest common factor, you are referring to 2, 3, or more numbers. (The word arithmetic is used by the general public to mean elementary. #Basic number theory definition of divides how to#
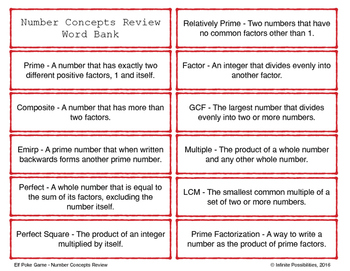
Now that you have understood how to get the factors of a number, it is going to be straightforward to to get the greatest common factor. Number theory is a branch of pure mathematics devoted primarily to the study of the integers. You can also make a factor tree to find all the factors.
In our example above, the factors started to repeat at 9 × 4 = 36 because you already has 4 × 9 = 36. Note that when the factors start to repeat, you have found them all.
0 kommentar(er)
